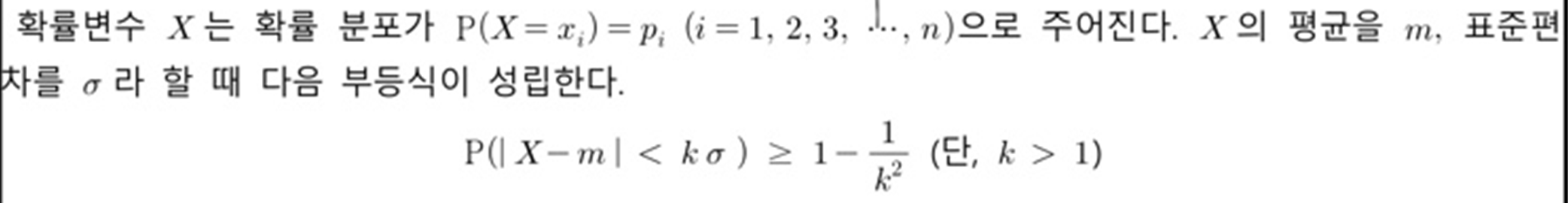
Chebyshev 부등식
저 버전도 있지만 개인적으로 위키백과에도 나와 있는

이게 더 깔끔하다.
직관적인 이해는 솔직히 다 될 것이다. k가 threshold와 같은 느낌의 변수인데,

이렇게 변수를 바꾸어 주면
사이에 저 x = 0 주위의 값 영역이 달라지면서

영역의 넓이가 달라지는 것이다. (k 변수에 대한 설명)
k가 커질수록 내부 영역의 넓이가 넓어지며, 외부 영역의 크기

(즉 이 확률이 작아지게 된다는 것이다)
이것에 대한 증명은 이런식으로 한다더라.
Proof
X 에 속하는 변량 x개가 있다고 가정하자.
이때,

퍼런 영역을 X1, 퍼런 영역 외에 다른 부분을 X2라 하자
이때 P(|X - m|) < kσ인 영역이 X1, P(|X - m|) >= kσ 인 부분이 X2이다.

딱히 어렵지 않은 증명이다.